车工锥度计算公式中的三角函数是保证加工精度的关键。通过合理的使用正弦函数和余弦函数,我们可以精确地计算出锥度的大小。同时,我们还需要考虑其他的因素,如材料的硬度、刀具的磨损等,以确保加工的效率和精度。
在机械加工中,车工锥度是一种常见的加工工艺。它的主要作用是使工件的一端直径小于另一端,形成一个锥形的形状。
这种加工方式在许多领域都有应用,如汽车、航空、军事等。在车工锥度的加工过程中,锥度计算公式是非常重要的,它是保证加工精度的关键。
本文将详细介绍车工锥度计算公式中的三角函数。
首先,我们需要了解什么是三角函数。在数学中,三角函数是用来描述三角形中各边和角之间关系的一组函数。它们主要包括正弦函数、余弦函数和正切函数。
在车工锥度加工中,我们主要使用正弦函数和余弦函数来计算锥度。
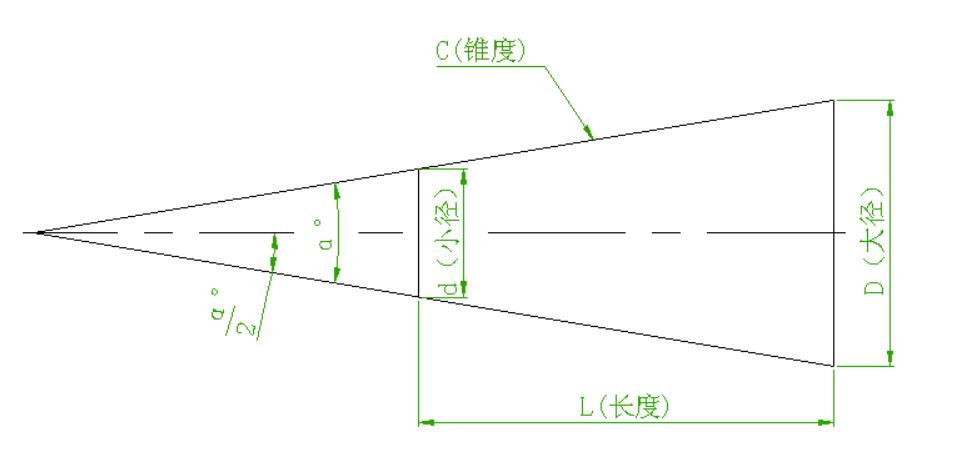
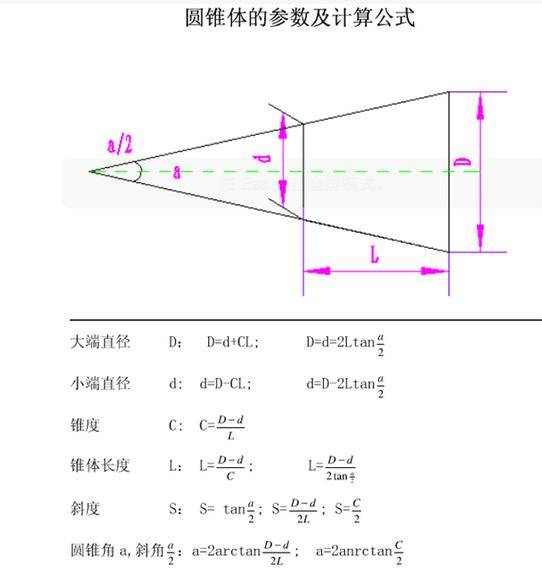
车工锥度的计算公式为:D=d*tana,其中D是大端直径,d是小端直径,a是锥度角。
这个公式告诉我们,锥度的大小是由大端直径、小端直径和锥度角三个因素决定的。而锥度角是通过正切函数计算出来的。
正切函数是三角函数的一种,它的定义是:当角度为直角时,正切函数的值等于对边的长度除以邻边的长度。
在车工锥度加工中,我们通常将锥度角设定为45度,这样可以使加工过程更加简单。因此,我们可以将锥度角a设定为45度,然后通过正切函数计算出锥度的大小。
在实际应用中,我们还需要考虑一些其他的因素,如材料的硬度、刀具的磨损等。
这些因素会影响到加工的精度和效率。因此,我们在使用车工锥度计算公式时,需要根据实际情况进行调整。
例如,如果材料的硬度较高,我们需要增加切削速度和进给量,以提高加工效率。
这时,我们可以通过调整锥度角a来改变切削速度和进给量。一般来说,锥度角越大,切削速度和进给量就越大。
但是,过大的锥度角可能会导致刀具过度磨损,影响加工精度。因此,我们需要根据实际情况进行适当的调整。
此外,刀具的磨损也会影响到加工的精度。在加工过程中,刀具会因为摩擦而逐渐磨损。
当刀具磨损到一定程度时,我们需要更换新的刀具。这时,我们可以通过测量刀具的磨损程度,然后通过车工锥度计算公式来计算出新的锥度大小。
总的来说,车工锥度计算公式中的三角函数是保证加工精度的关键。
通过合理的使用正弦函数和余弦函数,我们可以精确地计算出锥度的大小。
同时,我们还需要考虑其他的因素,如材料的硬度、刀具的磨损等,以确保加工的效率和精度。
只有这样,我们才能在车工锥度的加工过程中取得满意的效果。
