假设我们要找一个数x,使得x的平方大于2.我们可以写出这个条件的数学表达式:x^22.这个条件就是我们需要满足的必要条件。也就是说,只有当x满足这个条件时,我们才能说x的平方大于2.换句话说,如果x的平方不大于2.那么x就不满足我们的必要条件。
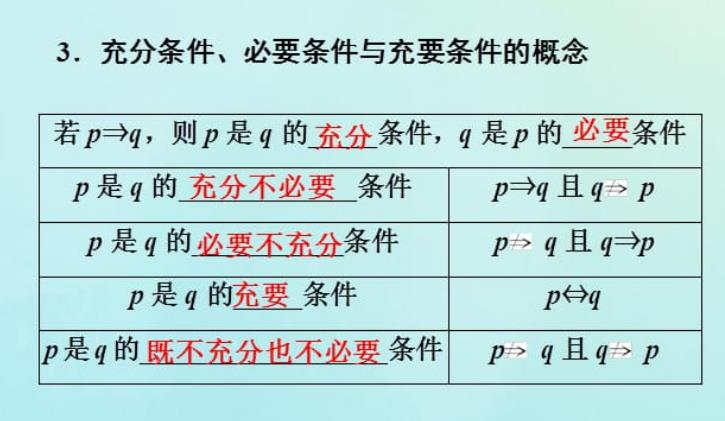
在数学中,必要条件和充分条件是两个基本的概念,它们在逻辑推理和证明中起着重要的作用。
然而,许多学生在学习这两个概念时,往往会混淆它们的含义和用法。因此,本文将通过举例来详细解释必要条件和充分条件的区别。
首先,我们来看一个例子。假设我们要找一个数x,使得x的平方大于2.我们可以写出这个条件的数学表达式:x^2 > 2.这个条件就是我们需要满足的必要条件。
也就是说,只有当x满足这个条件时,我们才能说x的平方大于2.换句话说,如果x的平方不大于2.那么x就不满足我们的必要条件。
然后,我们再来看一个充分条件的例子。假设我们要找一个数x,使得x的平方小于或等于2。
我们可以写出这个条件的数学表达式:x^2 ≤ 2.这个条件就是我们需要满足的充分条件。
也就是说,只要x满足这个条件,我们就能说x的平方小于或等于2.换句话说,如果x的平方大于2.那么x就不满足我们的充分条件。
从上面的两个例子,我们可以看出必要条件和充分条件的主要区别在于它们的推理方向。必要条件是从结果推导出原因,而充分条件则是从原因推导出结果。
换句话说,必要条件是一种“如果不……那么不……”的逻辑关系,而充分条件则是一种“如果……那么……”的逻辑关系。

例如,如果我们说“一个人要成为医生,他必须通过医学院的考试”,那么“通过医学院的考试”就是我们成为医生的必要条件。
因为只有通过了医学院的考试,我们才能成为医生。这就是从结果(成为医生)推导出原因(通过医学院的考试)。
相反,如果我们说“如果一个人通过了医学院的考试,那么他就可以成为医生”,那么“通过医学院的考试”就是我们成为医生的充分条件。因为只要通过了医学院的考试,我们就可以成为医生。这就是从原因(通过医学院的考试)推导出结果(成为医生)。
在实际的数学问题中,必要条件和充分条件的判断是非常重要的。例如,在解决不等式问题时,我们需要找出使不等式成立的充分条件。
在解决函数问题时,我们需要找出使函数成立的充分条件和必要条件;在解决几何问题时,我们需要找出使几何性质成立的充分条件和必要条件等。

总的来说,必要条件和充分条件是数学中的基本概念,它们在逻辑推理和证明中起着重要的作用。
理解并掌握这两个概念,对于提高我们的数学素养和解决问题的能力是非常有帮助的。希望本文的解释和举例能够帮助大家更好地理解和区分必要条件和充分条件。
