总的来说,欧几里得的勾股定理是数学史上的一个重要成就。他的证明方法不仅揭示了直角三角形的一些基本性质,而且为后来的数学家提供了宝贵的启示。他的工作对于数学的发展产生了深远的影响,被誉为“数学之父”。
欧几里得,古希腊数学家,被誉为几何学的奠基人。他的许多贡献都集中在数学的各个方面,包括算术、代数、几何和三角学。其中,他最为人所知的贡献之一就是证明了勾股定理。
欧几里得的生平
公元前300年左右,欧几里得出生在希腊的一个贫穷家庭。他的父亲是一位木匠,母亲则是一位织布女工。尽管生活困苦,但欧几里得的父母始终鼓励他追求知识。

欧几里得从小就表现出了对数学的热爱。他阅读了许多古代的数学著作,并开始自己研究数学。他的研究成果很快就得到了老师和同学的认可。
然而,欧几里得并没有满足于此。他知道,要真正理解数学的本质,还需要更深入的研究。于是,他决定离开家乡,前往雅典,寻求更多的知识和启示。
欧几里得的证明
在雅典,欧几里得遇到了许多杰出的数学家,如毕达哥拉斯、阿基米德和欧拉等。他们都是欧几里得的朋友和导师,对他的研究产生了深远的影响。
欧几里得的主要工作是证明勾股定理。这个定理的内容是:在一个直角三角形中,斜边的平方等于两直角边的平方之和。这个定理在古代就被广泛接受,但在后来的岁月里,由于各种原因,它的地位逐渐被削弱。
为了证明这个定理,欧几里得提出了一种叫做“三边中垂线”的方法。这种方法的基本思想是:如果一个直角三角形的斜边长为c,那么在这个三角形中,存在一条与斜边垂直且长度为c/2的中垂线。
这条中垂线将直角三角形分为两个直角三角形,其中一个直角三角形的两个直角边的平方和等于斜边的平方。因此,我们可以说,斜边的平方等于两直角边的平方之和。
欧几里得的这个方法非常巧妙,它不仅证明了勾股定理,而且还揭示了直角三角形的一些基本性质。这个方法很快在数学界引起了轰动,成为了数学史上的一个重要里程碑。
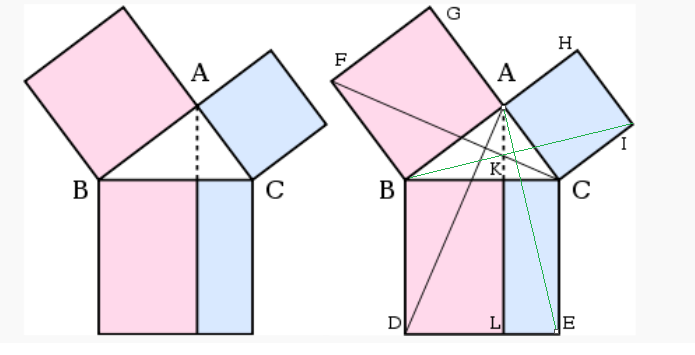
欧几里得的影响
欧几里得的勾股定理不仅在当时产生了深远的影响,而且在后世也一直被广泛接受。这是因为,勾股定理揭示了直角三角形的一些基本性质,这些性质在数学的其他领域也有广泛的应用。
此外,欧几里得的证明方法也非常独特。他的方法是通过观察和推理,而不是通过直接的计算。这种方法使得人们能够更好地理解和掌握数学的知识。
总的来说,欧几里得的勾股定理是数学史上的一个重要成就。他的证明方法不仅揭示了直角三角形的一些基本性质,而且为后来的数学家提供了宝贵的启示。
他的工作对于数学的发展产生了深远的影响,被誉为“数学之父”。
