总之,对边比斜边是一个关于直角三角形的概念,它描述了直角三角形中对边与斜边之间的比例关系。然而,这个概念并没有直接涉及到三角函数。在某些情况下,我们可以使用三角函数来描述边长之间的关系,但这种关系并不是基于勾股定理的。
在几何学中,三角形是最基本的图形之一。一个三角形由三条线段组成,这三条线段被称为三角形的边。
在直角三角形中,有一条边(我们称之为“对边”)与另一条边(我们称之为“斜边”)之间的比例是一个特定的常数。这个常数被称为勾股定理,它可以用以下公式表示:
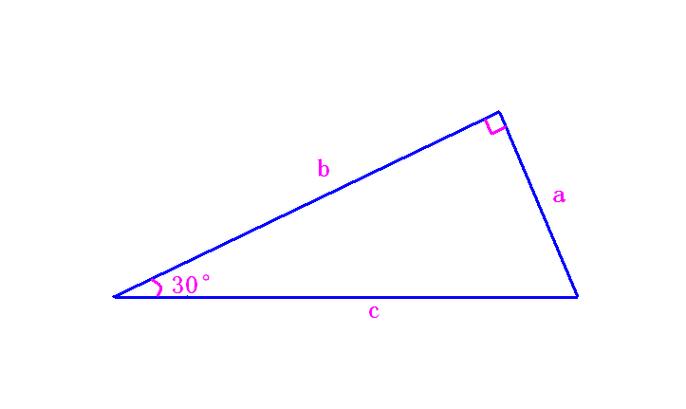
c² = a² + b²
其中,a 和 b 分别是直角三角形的两个直角边,c 是斜边。根据勾股定理,我们可以得出以下结论:
如果一个三角形的两条直角边的平方和等于斜边的平方,那么这个三角形就是直角三角形。
在一个直角三角形中,对边的长度等于斜边长度的一半。
在一个直角三角形中,对边与斜边之间的比例是一个常数,这个常数等于斜边的平方除以对边和斜边的平方和。
然而,这个结论并没有直接涉及到三角函数。实际上,直角三角形的性质与三角函数没有直接关系。
三角函数通常用于描述角度之间的关系,而不是描述边长之间的关系。但是,在某些情况下,我们可以使用三角函数来描述边长之间的关系。
例如,我们可以使用正弦函数来描述一个角的正弦值与该角的边长之间的关系。在这种情况下,我们可以将勾股定理中的对边与斜边之间的比例表示为:
sin(θ) = c / a
其中,θ 是与对边相邻的角,c 是斜边的长度,a 是对边的长度。这个公式表明,当一个角的正弦值与该角的边长相同时,对边与斜边之间的比例是一个常数。
然而,这个公式并不能直接应用于所有的直角三角形,因为并不是所有的角都有相同的正弦值。
总之,对边比斜边是一个关于直角三角形的概念,它描述了直角三角形中对边与斜边之间的比例关系。然而,这个概念并没有直接涉及到三角函数。
在某些情况下,我们可以使用三角函数来描述边长之间的关系,但这种关系并不是基于勾股定理的。
