在数学中,集合是一个包含一组唯一元素的无序集合。子集是原始集合的一部分,可以是从原始集合中删除一个或多个元素得到的新集合。真子集和非空子集是子集的两个重要类别。
真子集的概念
真子集是指从原始集合中删除一个或多个元素得到的新集合。
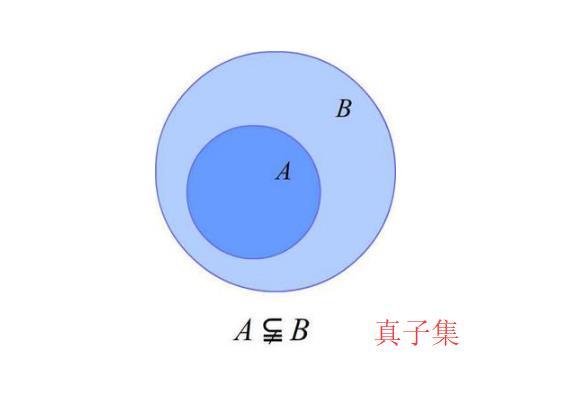
换句话说,如果一个集合A是另一个集合B的子集,那么A就是B的一个真子集。真子集与子集的关系是:如果A是B的子集,且A不等于B,则A是B的一个真子集;否则,A不是B的真子集。
真子集的定义可以通过以下方式表示:如果集合A的所有元素都在集合B中,并且集合A至少包含一个不在集合B中的元素,那么A就是B的一个真子集。这个定义可以用数学符号表示为:A ⊆ B ∧ A ≠ B。
非空子集的概念
非空子集是指至少包含一个元素的子集。换句话说,如果一个集合A至少包含一个元素,那么A就是一个非空子集。非空子集与空集的关系是:非空子集不能等于空集。
非空子集的定义可以通过以下方式表示:如果集合A至少包含一个元素,那么A就是一个非空子集。这个定义可以用数学符号表示为:A ≠ ∅。
真子集和非空子集的应用
真子集和非空子集在许多领域都有广泛的应用,例如数学、计算机科学、生物学等。以下是一些例子:
1.在数学中,真子集通常用于描述集合之间的关系,例如集合的幂集、笛卡尔积等。
2.在计算机科学中,真子集可以用于算法的时间复杂度分析,例如排序算法、搜索算法等。
3.在生物学中,真子集可以用于描述基因之间的相互作用关系,例如基因调控网络等。
总结
真子集和非空子集是集合论中的两个重要概念,它们在数学、计算机科学、生物学等领域都有广泛的应用。了解真子集和非空子集的概念和定义,可以帮助我们更好地理解和应用这些概念和理论。
