椭圆离心率计算公式是什么?
椭圆离心率是描述椭圆形状的一个重要参数。在数学中,椭圆的离心率定义为长轴(主轴)与短轴(次轴)之间的比值。这个比值可以用以下公式表示:
e = √(1 - (b²/a²))
其中,a是椭圆的长半轴长度,b是椭圆的短半轴长度,e是椭圆的离心率。
如何推导椭圆离心率的计算公式?
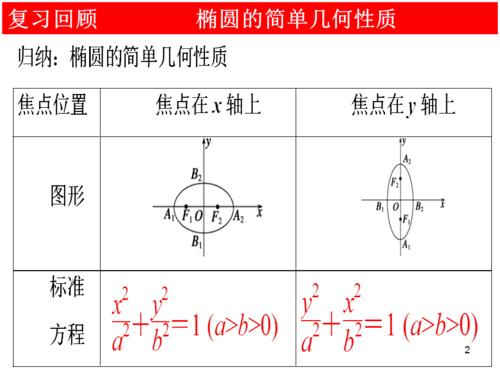
椭圆离心率的计算公式是基于椭圆的定义和性质推导出来的。首先,我们知道椭圆是由两个相等的圆相交形成的,这两个圆的半径分别是长半轴和短半轴。因此,我们可以得到以下等式:
a² = b² + r²
其中,r是椭圆的中心到任意一点的距离,也就是椭圆的焦距。根据椭圆的定义,我们知道焦距等于长半轴和短半轴的差的一半,即:
f = (a - b) / 2
将焦距代入上式,我们可以得到:
a² = f² + r²
然后,我们可以将a和b的值代入第一个等式,得到:
a² = (f + r)² + r²
化简后,我们可以得到:
a² = (f + r)(f + r)
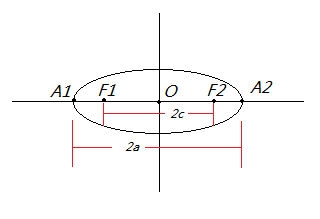
由于f和r都是相等的,所以:
(f + r)(f + r) = a²
进一步简化,我们可以得到:
2af + 2ar = a²
化简后,我们可以得到:
2af + ar = a²
