一、引言
微积分是数学的一个分支,主要研究函数的极限、连续性、可微性和积分等问题。它在物理学、工程学、经济学等许多领域都有广泛的应用。
其中,微积分在几何学中的应用尤为突出,例如在推导球的表面积公式中就发挥了重要作用。本文将详细介绍如何使用微积分来推导球的表面积公式。
二、球的表面积公式
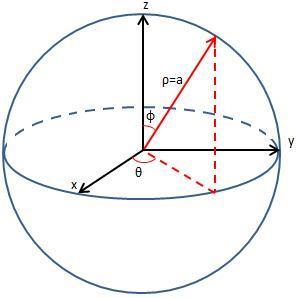
球的表面积公式是所有曲面面积公式中最简单的一个,它的形式为A=4πr²,其中A是球的表面积,r是球的半径。这个公式看似简单,但其背后的推导过程却涉及到了微积分的一些重要概念,如极限、积分和面积元素等。
三、微积分的基本概念
在推导球的表面积公式之前,我们先来回顾一下微积分的一些基本概念。
1. 极限
极限是微积分的基础概念,它描述了一个函数在某一点附近的行为。如果一个函数在某一点的极限存在,那么我们就说这个函数在这一点是连续的。
2. 积分
积分是微积分的另一个重要概念,它是对无穷小量的求和。在微积分中,我们通常用∫表示积分,并用f(x)dx表示对函数f(x)在区间[a,b]上的积分。
3. 面积元素
面积元素是微积分中的一个重要概念,它是对二维平面上的一个微小区域的度量。
在二维平面上,面积元素通常表示为dA=dxdy或dA=rdθdφ,其中dxdy表示矩形区域的元素,rdθdφ表示极坐标区域的元素。
四、球的表面积公式的推导
有了上述的基础知识,我们就可以开始推导球的表面积公式了。
首先,我们考虑一个半径为r的球,其表面是由无数个微小的圆环组成的。
每个圆环的宽度可以看作是dx,高度可以看作是dy。由于球的表面是均匀的,所以每个圆环的面积都可以看作是一个微小的矩形区域,其面积为dxdy。
然后,我们考虑这些微小的圆环的总面积。由于圆环的数量是无穷多的,所以我们可以用积分来表示这个总面积,即∫dxdy。这就是球的表面积的第一个部分。
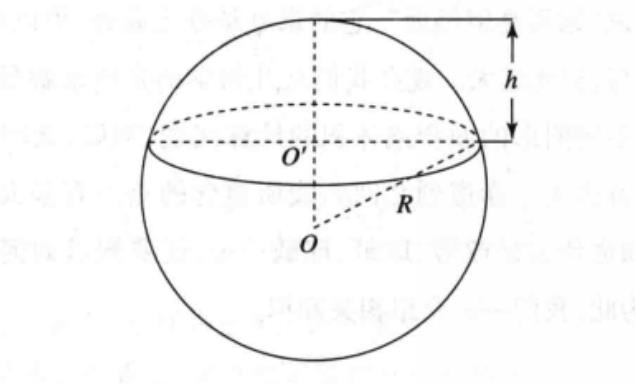
接下来,我们考虑球的另一部分表面,即两个半球的表面。每个半球的表面是由无数个微小的圆弧组成的。
每个圆弧的长度可以看作是rdθ,其中θ是圆弧的中心角。由于半球的表面是均匀的,所以每个圆弧的面积都可以看作是一个微小的扇形区域,其面积为rdθdθ。
最后,我们考虑这些微小的圆弧的总面积。由于圆弧的数量是无穷多的,所以我们可以用积分来表示这个总面积,即∫rdθdθ。这就是球的表面积的第二个部分。
五、结论
通过以上的推导,我们得到了球的表面积公式A=4πr²。
这个公式虽然看起来简单,但其背后的推导过程却涉及到了微积分的一些重要概念,如极限、积分和面积元素等。这也体现了微积分在几何学中的重要作用。
