以下这些结论是高中数学中复数部分的基础,理解和掌握这些结论对于解决复数相关的问题有着重要的作用。在学习过程中,我们可以通过大量的练习来加深对这些结论的理解和记忆,从而提高我们解决复数问题的能力。
以下这些结论是高中数学中复数部分的基础,理解和掌握这些结论对于解决复数相关的问题有着重要的作用。在学习过程中,我们可以通过大量的练习来加深对这些结论的理解和记忆,从而提高我们解决复数问题的能力。高中数学中的复数部分是相当重要的一部分,它涉及到许多基本的概念和定理。对于复数,我们需要理解它的基础知识点,并掌握一些常用的结论。以下是复数的15个常用结论:
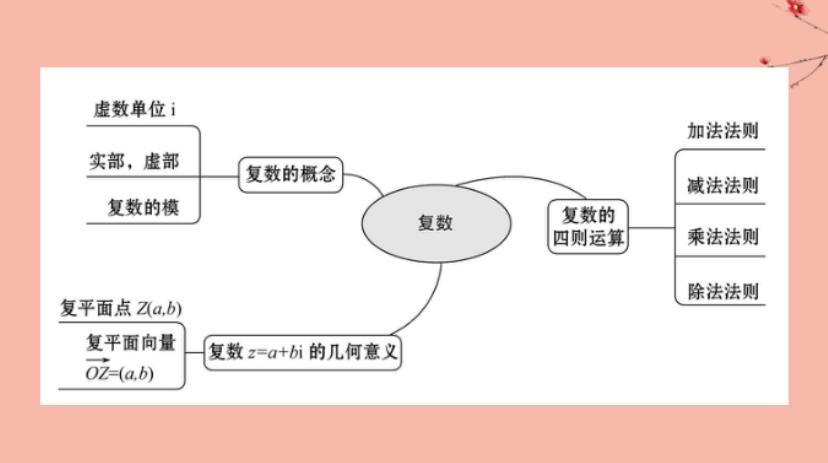
1. 复数的加法和减法:两个复数相加或相减时,实部和虚部分别进行加减运算。
2. 复数的乘法:两个复数相乘时,(a+bi)(c+di)=ac-bd+(ad+bc)i。
3. 复数的除法:两个复数相除时,(a+bi)/(c+di)=(ac-bd+(ad+bc)i)/(c²+d²)。
4. 共轭复数:一个复数的共轭复数是将虚部变为相反数得到的新复数。
5. 模长公式:一个复数z=a+bi的模长|z|定义为√(a²+b²)。
6. 复数的三角形式:一个复数可以表示为r(\cosθ+i\sinθ),其中r是模长,θ是辐角。
7. 复数的指数形式:e^(ix)=cosx+i\sinx。
8. 欧拉公式:e^(ix)=cosx+i\sinx,这个公式将五个最重要的数学常数(0.1.π,e,i)联系在一起。
9. 复数的幂运算:(a+bi)^n=C(n,0)a⁰+C(n,1)a¹*i+C(n,2)a²*i²+...+C(n,n-1)a⁹*iⁿ-1+C(n,n)a¹⁰*i¹⁰。
10. 复数的对数运算:log_a(z)=log_a(r)+ilog_a(\tanθ)。
11. 复数的绝对值不等式:|z₁±z₂|\leq|z₁|+|z₂|。
12. 复数的四则运算法则:(a+bi)(c+di)=ac-bd+(ad+bc)i。
13. 复数的三角形式的极坐标表示:r(cosθ+i\sinθ)=r(\cosφ\cosθ+i\cosφ\sinθ+i\sinφ\sinθ)。
14. 复数的模长的平方等于实部和虚部的平方和:|z|²=a²+b²。
15. 复数的模长小于等于其实部和虚部的平方和:|z|\leq a²+b²。
以上这些结论是高中数学中复数部分的基础,理解和掌握这些结论对于解决复数相关的问题有着重要的作用。

在学习过程中,我们可以通过大量的练习来加深对这些结论的理解和记忆,从而提高我们解决复数问题的能力。
同时,我们也需要理解这些结论背后的数学原理,这样才能在遇到复杂问题时,灵活运用这些结论,找到解决问题的方法。
